Tic-Tac-Toe is a cool game when talking about Game Theory. It’s an adversarial game (where both players have opposite goals), in which a decision from each player influences the whole game state.
Today, we’re going to learn how to encode a match of Tic-Tac-Toe in a single number by using Bitwise operations. Our requirements are:
- There cannot be any previous knowledge about the game. Only that number.
- That means that we cannot simply count each game state and assign an ID to it.
- We cannot use structures / objects to make this simpler.
The number of game states that Tic-Tac-Toe has is $ 765 $1, we could assign a unique number to each one of those states only using a 9.58-bit unsigned integer. But that’s boring, doesn’t meet our requirements and the worst of all: Memory intensive
We don’t want to use much memory here; not because of real concerns, but because of imaginary ones.
So, we need a way to indicate how does the game look, using a very limited number of bits, $\leq 128$, so that it can fit in a single Rust u128.
Note that we don’t know yet the number of bits we need (we only know that it needs to be less than 128), so we’ll define $“n”$ as the number of bits necessary.
A cluster inside a cluster inside a…
Nobody said that we need to think of our bytes as a single number (well, I kinda did). So we’re going to split our bits into two $\frac{n}{2}$-bit clusters. The first cluster will contain positions for Player 1, and the second cluster will contain positions for Player 2.

Now, we can create more clusters inside those clusters! We’ll make 9 more clusters inside each one of those clusters to store each one of the squares. We’ll use 2 bits to represent a single square. Doesn’t trigger your programmer built-alarms? Using 4 possible values to represent 3 possibilites?
Getting to the real deal
Let’s imagine we have this board:
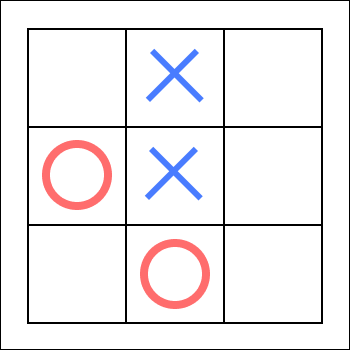
Having the following distribution:
| A1 | B1 | C1 |
| A2 | B2 | C2 |
| A3 | B3 | C3 |
This would be the translation into our new format:
- A1 ->
00(Empty) - B1 ->
01(Cross) - C1 ->
00(Empty) - A2 ->
10(Circle) - B2 ->
01(Cross) - C2 ->
00(Empty) - A3 ->
00(Empty) - B3 ->
10(Circle) - C3 ->
00(Empty)
So now we know, the ID for this specific board is ✨ 18696 ✨ But… this data isn’t compressed, we would use 18 total bits, innacceptable!
Or… is it?
I just made some benchmark using the Rust’s std::mem::size_of function. And so, checking the following simple struct:
struct Board {
pub board: [State; 9]
}
Turns out it uses 9 bytes! That’s 4 times larger than our required 18-bit encoded number. I guess it was compressed after all.
use std::mem::size_of;
enum State {
Empty,
Cross,
Circle,
}
struct Board {
pub board: [State; 9]
}
impl Board {
pub fn is_tied(&self) -> bool {
for state in &self.board {
if matches!(state, State::Empty) {
return false;
}
}
true
}
}
fn main() {
println!("{}", size_of::<Board>());
}